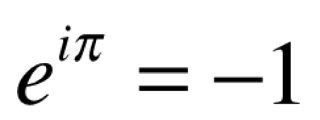Zahlen sind abstrakte Einheiten die die Vielzahl der Dinge darstellen. Sie werden mit Symbolen dargestellt. Im Laufe der Entwicklung der verschiedenen Kulturen, die die menschliche Geschichte prägten, wurden verschieden Symbolsysteme verwendet.
Die Urbevölkerungen der Erde kannten nur die Zahlen eins, zwei und drei. Auch primitive Bevölkerungen wie die Pygmäen Afrikas, die Urbevölkerungen Australiens oder die Botocudos aus dem Amazonas kennen nur diese drei Zahlen wobei die Zahl Drei eigentlich die Mehrzahl bedeutet.
So wurde diesen Zahlen auch symbolische Wertung gegeben. Die Zahl Eins meistens mit einer senkrechten Linie dargestellt symbolisiert den Menschen der als einziges lebendes Geschöpf aufrecht gehen kann oder durch die Symbolisierung des Phallus das Männliche. Die Zahl Zwei symbolisierte schon immer den Dualismus zwischen Mann und Frau, zwischen Leben und Tod, zwischen Gutem und Bösem. Die Zahl Drei symbolisierte die Vielzahl. So wurde im alten Ägypten um die Mehrzahl eines Gegenstandes darzustellen, das den Gegenstand symbolisierende Hyroglyph dreimal wiederholt.
Auch in vielen modernen Sprachen gibt es noch Spuren dieser Bedeutung. So haben im Französischem die Worte “trois” (drei) und “tres” (viel) die gleiche etymologische Wurzel. So bedeutet im Englischen das Wort “thrice” sowohl “dreimal” als auch “vielmals”. Die alte sächsische Wurzel “thria” aus der das deutsche “drei” oder das englische “three” abstammt ist etymologisch mit dem fränkischen “throp” verwandt aus dem Worte wie das französische “trop” das italienische “troppo” das deutsche “Truppe” abstammen.
Die Zahlen wurden in diesen primitiven Bevölkerungen mit dem Wiederholen eines einzigen Symbols, meistens dem senkrechten Strich symbolisiert. So stellt man “zwei” mit zwei, “drei” mit drei, “vier” mit vier Strichen dar. Auch die nachfolgenden Zahlen wurden mit Strichen symbolisiert. Das Lesen dieser Zahlen war sicher nicht so einfach auch weil unser Hirn relativ einfach bis vier gleiche Symbole erkennt bei fünf wir aber schön zum Zählen gezwungen sind. Dies brachte sehr bald zu Definition einer anderen Schreibweise ab der Zahl “Fünf”. So entwickelten sich die Zahlensysteme der Ägypter und der Kreteser die um “fünf” zu schreiben auf verschiedenen Zeilen die Zahlen zwei und drei schrieben. Später kam es zur Einführung eines eignes Symbol für die Zahl fünf , das die offene Hand symbolisierende “V”, und des additiven Symbolsystems so wie es uns von den Römischen Zahlen bekannt ist. Diese System ermöglichte mit der Einführung neuer Symbole für die Zahlen zehn “X” (zweimal “V”) fünfzig “L”, hundert “C” ,fünfhundert “D” und tausend “M” das Darstellen auch relativ großen Zahlen. Auch ermöglichte dieses Zahlensystem mit Hilfe des “Abbacus”, dem antiken Rechenbrett, das Ausführen mathematischer Operationen wie das Addieren und das Subtrahierenden und, wenn auch auf sehr komplizierten Art und Weise, auch das Multiplizieren und Dividieren. Die Einführung eines Symbolsystemes hatte zur Entwicklung von Regeln geführt die das Verständnis von Zusammenhängen förderten. Das Verständnis dieser Zusammenhänge hatte es ermöglicht mit Zahlen Operationen durchzuführen die im Handel und in der Buchführung große Fortschritte brachte. Diese Entwicklung wird mit der Erfindung der arabischen Ziffern unter Verwendung des Stellenwertsystems noch markanter.
Zwischen den Jahren 800 bis 825 schrieb ein ostarabischer Mathematiker namens Muhamad Ibn Misa Alchworizimi aus Bagdad das grundlegende Werk über das Rechnen mit den indischen (den sogenannten arabischen Zahlen). In diesem Werk erscheint erstmals die Null die mit einem kleinen Kreis symbolisiert wurde.
Auf verschiedenen Wege durch die Kreuzzüge aber auch durch die arabischen Hochschulen in Toledo, Sevilla, Granada gelangten die arabischen Werke in lateinischer Übersetzung zur Kenntnis der abendländischen Gelehrten und unter diesen Werken auch das Buch Alchworizimis über die indischen Ziffern, die von Leonardo Fibonacci aus Pisa im Liber Abaci um 1202 übernommen wurden. Die Algorithmiker, so wurden, vom Namen Alchworizimis, die Verfechter des neuen Symbolsystems genannt, führten unter den Namen Algorithmus das indische Ziffernsystem mit Stellenwertberücksichtigung im Abendland ein.
Die Gegenüberstellung zwischen den Abbazisten, den Verfechter des Römischen Zahlensystems und des Abbacus, und den Algorithmiker markierte die Kulturgeschichte des späten Mittelalters bis zur Renaissance. Die Algorithmiker lieferten die Ergebnisse von Rechenoperationen über geheimnisvolle Symbole (unseren heutigen Zahlen) die es gestatteten die verwickeltsten und größten Rechnungen mit unfehlbarer Sicherheit durchzuführen während die Abbazisten mühevoll die Kügelchen am Rechenbrett (Abaccus) herschoben.
Die katholische Kirche, die um ihr Monopol in der Lehre und Erziehung bangte, war gegen eine Demokratisierung des Kalküls das bis dort Monopol einer privilegierten Kaste war. Dies brachte zu einem eklesiastischem Veto der neuen Methoden bis ins XV Jahrhundert. Die Algoristen mußten also im geheimen mit ihren “Ziffern” (Dieses Wort hat seinen Ursprung im arabischen Sifir (das Leere) mit dem die Null gekennzeichnet wurde) umgehen. Heute noch nennt man “Chiffrieren” die Umwandlung eines Textes mittels eines Geheimcodes.
Die Aussagekraft des neuen Symbolsytems war aber so stark das es, trotz der starken kirchlichen Opposition, sich langsam durchsetzte und nach der Französischen Revolution, die den Abbacus in den Schulen und Staatsämter verbat, endlich der Menschheit seinen vollen Dienst leisten konnte. Das Indische Zahlensystem ist ein klares Beispiel wie ein Symbolsystem, das aus Symbolen und Regeln die diese Symbole verwalten besteht, maßgebend für die Weiterentwicklung der Wissenschaft ist und somit das Verständnis der Regeln und Gesetze, die die Natur verwalten, fördert.
Das neue Zahlensystem ermöglichte die Geometrischen Intuitionen der Griechen zu vervollständigen und ermöglichte somit das Blühen der Wissenschaften und den geistigen Fortschritt während des Illuminismus bis zur heutigen Zeit.
Eins nach dem anderem wurden die maßgebenden Meilensteine der modernen Mathematik gesetzt. Die Symboltheorie wurde durch Gottfried Willhelm Leibnitz, der von 1646 bis 1716 lebte und Anhänger des Rosen-Kreuzes war auf soliden logischen Fundamente gesetzt. Er entwickelte die Lehre der Symbole die er “Kabbala Vera” nannte. Die mathematischen Zeichen sind maßgebende Bestandteile in dem Leibnizchen Symbol-kalkül. Die Anordnung der Symbole, ihre Form tragen einen wesentlichen Beitrag zur Algorithmik (das Wort erhält nun eine neue Bedeutung die sich nicht nur mehr auf die Arabischen Ziffern bezieht sondern im Allgemeinen Lösungsmethoden mittels Symbolsystemen darstellt). Der wichtigste Beitrag Leibnitz im Bereich der Naturwissenschaften ist das Symbolische Kalkül auch Sublimes Kalkül genannt, das endlich das Paradox des Achilles und der Schildkröte von Zenon löste.
Das Symbolische Kalkül wurde das Fundament der moderne mathematische Differential und Integralrechnung. Diese mathematische Theorie ermöglichte Newtons Gravitation Theorie und im 19 Jahrhundert die Maxwellschen Gleichungen die die unsichtbare Welt des Elektromagnetismus symbolisch in geschlossener und eleganter Weise darstellte. Die Auswirkungen dieser Theorien stehen vor unseren Augen. Wieder zeigt es sich das wenn Symbole das “Wesen” der Natur treffen diese ein gewaltiges Mittel zur Weiterentdeckung und Aufschlüsselung der wunderbaren logischen Struktur des Universums werden.
Ein weiterer Fortschritt kam durch andere große Mathematiker wie Leonhard Euler (1707-1783) und Friedrich Gauss (1777-1855), mit der Einführung der Imaginären Zahlen. Diese entstanden aus der Definition der quadratischen Wurzel der Zahl -1. Wie bekannt ist die Wurzel einer Zahl jene Zahl die, wenn mit sich selber multipliziert, die Ausgangszahl ergibt. Nun gibt jede Zahl ob positiv oder negativ wenn mit sich selbst multipliziert ein positives Ergebnis. Diese Eigenschaft der Zahlenalgebra macht die Suche nach der Wurzel einer negativen Zahl unmöglich. Euler löste das Problem indem er diese unmögliche Zahlengröße mit dem Symbol i darstellte und um diese imaginäre Zahl eine formelle Algebra entwickelte die auch Algebra der komplexen Zahlen genannt wurde. Dieser Formalismus ging weit über die Erwartungen Leonhard Eulers und der Mathematiker die auch später ihren Beitrag zur komplexen Algebra und Funktionstheorie gaben.
Heute basieren große Bereiche der Naturwissenschaften auf der Komplexen Algebra . So wie zum Beispiel die Signaltheorie in der Elektronik, die Aerodynamik, die Fluidodynamik, Teile der Quantenmechanik und der allgemeine Relativitätstheorie, wo die Zeitliche Dimension des Raum-Zeit Kontinuums als imaginäre Dimension dargestellt wird. Wieder hatte ein symbolischer Formalismus “getroffen” und somit wieder viele Geheimnisse der logischen Struktur unseres Universums entlarvt. Der symbolische Formalismus wird das Mittel zur Erkenntnis. Die Wissenschaftler bemühen sich, nicht immer bewußt, beim formulieren ihrer Theorien symbolische Darstellungen zu finden die nicht nur dem wissenschaftlichen Kriterien der Logik und Kohärenz entsprechen sondern die resultierende Formel und ihre symbolische Darstellung muß auch andere Kriterien erfüllen: Einfachheit, Eleganz, Schönheit. Nur dann hat es sich gezeigt wird die dazugehörende Theorie wissenschaftlichen Erfolg haben. Es ist als ob dann die Symbole durch eigener Kraft neue Aspekte der Natur enthüllen.
Abschließend möchte ich ein einfaches Beispiel bringen. Es handelt sich dabei um einen von Leonhard Euler, basierend auf Studien von Abraham de Moiree, bewiesener Satz. Dieser bindet unter sich heterogene Größen:
Als erste Größe die Kreiszahl pi (3,14159.....) welche mit dem griechischen Buchstaben π dargestellt wird. Diese Zahl symbolisiert das Verhältnis zwischen Kreis und seinen Durchmesser. Es ist eine sogenannte Transzendente Zahl da sie nicht in geschlossener Form mit den natürlichen Zahlen darstellen läßt. Das bedeutet das der Kreis mit seinem Durchmesser nicht in numerischer Relation gebracht werden kann. Ich kann den Kreis und seinen Durchmesser in unendlich kleine Teile aufteilen, werde aber nie auf einen gemeinsamen Teiler kommen. Das bedeutet das die Zahl π unendlich viele Stellen hinter den Komma hat.
Die Zahl π symbolisiert den Kreis und die Kugel. Das ewig Statische das aus jedem Blickwinkel gleich aussieht. Die Kugel ist in sich vollkommen. Diese Perfektion ertönt aus dem Vorsokratischem Fragment des Empedokles:
“Aber er, von allen Seite sich selbst gleich und überall endlos, Sphairos, der kugelförmige, über die ringsum herrschende Einsamkeit von frohem Stolz erfüllt”
Die zweite Große die wir in Betracht ziehen ist die Zahl e (2.7183...), auch Eulersche Zahl genannt. auch sie ist auch eine transzendente Zahl mit unendlich vielen Kommastellen die aber in einem ganz anderen Kontext entsteht. Sie prägt die sogenannte Wachstumkurve oder exponentielle Funktion. Sie ist überall dort zu treffen wo etwas wächst: ob es um verzinstes Kapital geht oder um Vermehrung von Zellen. Dort überall wo etwas wächst, wo etwas wird kommt immer die Zahl e zum Vorschein.
Diese zwei Größen die auf so unterschiedlicher Weise entstehen wurden durch Euler in Relation gesetzt. Und zwar beweist Euler daß:
Diese Relation verbindet unter sich 4 Größen. Die Zahlen π, e, 1 und i, die imaginäre Zahl die die Wurzel aus -1 symbolisiert, werden in einer bedeutungsvollen und eleganten Weise in Relation gesetzt. Sie verblüfft gleichfalls den Mathematiker, den Philosoph, den Wissenschaftler den Mystiker. Sie verbindet das “Werden” mit dem statischen “Sein” über das “Unmögliche” mit der “Negation” und der “Einheit”. Sie ist absolut paradox und trotzdem beweisbar im Kontext des mathematischen Formalismus und somit “wahr”. Die Formel reißt den Schleier, der das Absolute verbirgt, auf und läßt uns die Schönheit und die Komplexität des Universums ahnen.