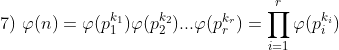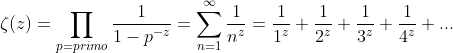La poetica dei numeri primi

La poetica dei numeri primi

Nel 2019 Matera è stata capitale europea della cultura. Il comitato organizzatore della manifestazione incaricò Piergiorgio Odifreddi di organizzare alcuni eventi di natura matematica inseriti in un progetto dal nome accattivante di “la poetica dei numeri primi”. Il progetto si sviluppava in due diversi sedi, Matera e Metaponto e doveva attraverso linguaggi diversi, quello della divulgazione e quello dell’arte, riproporre l’eredità intellettuale di Pitagora che proprio a Metaponto aveva trovato il suo ultimo riposo. Tra gli ospiti erano previsti, tra gli altri, il premio Nobel per la letteratura John Coetzee, scienziati del valore di Guido Tonelli e Ian Stewart e il più noto divulgatore italiano Pietro Angela. Era prevista anche una sezione dedicata all’arte ispirata alla matematica e Piergiorgio mi chiese di allestire una mostra sull’arte delle tassellazioni, l'uso di tasselli regolari, geometrici o dalla forma animata, per riempire il piano senza lasciare spazi vuoti. In particolare la mostra doveva, oltre a illustrare la teoria alla base della tassellazione regolare, esporre opere di artisti che si erano cimentati in questa difficile arte ed in particolar modo le opere dell’indiscusso maestro di questa disciplina: M.C Escher. Oltre alla mostra sulle tassellazioni, nella sezione dedicata all’arte erano previste altre mostre dedicate ad artisti che si erano ispirati alla matematica. Era prevista una mostra di Ugo Nespolo, una retrospettiva di Aldo Spizzichino e una mostra dell’artista veneziano Tobia Ravà, che per l’occasione aveva preparato la mostra “Elementi di calcolo trascendentale”. Conoscevo l’arte di Tobia basata sulla tradizione esoterica ebraica, la cabbala, ed in particolare sul metodo di analisi delle scritture chiamato ghematria. Questo metodo sfrutta la proprietà della notazione numerica ebraica, che rappresenta i numeri, senza usare simboli speciali ma con le lettere dell'alfabeto in una notazione additiva. Ogni parola scritta quindi oltre a rappresentare un concetto rappresenta quindi anche un numero. Questo permette lo studio delle parole e dei testi anche dal punto di vista numerologico. Ogni numero associato ad una parola può inoltre essere ridotto ad un unico numero minore di 10 sommando ripetutamente le cifre fino ottenere un numero ad una sola cifra. In matematica questo processo definisce la radice numerica di un numero. Tobia, con una tecnica divisionista, usava i numeri per formare le figure e visto che ai numeri corrispondevano parole e concetti, questi non erano disposti a caso, ma definivano percorsi descrittivi che formavano un ulteriore strato interpretativo dell'opera.

Partecipava alla manifestazione anche Claudio Bartocci docente di fisica matematica e storia della matematica all'università d Genova, che aveva per l’occasione insieme a Luigi Civalleri allestito la mostra dal titolo: “Numeri nel tempo. Contare, misurare, calcolare”. Era stato Claudio a farmi conoscere 12 anni fa Tobia, infatti sul frontespizio di una antologia di racconti matematici del edita da Enaudi nel 2006 e da lui curata, era raffigurata il volto di una donna realizzato da Tobia con numeri colorati. Incuriosito dall’uso dei numeri per raffigurare figure mi misi in contatto con Tobia, diventando in seguito un estimatore della sua particolare arte.

Il giorno prima del solstizio ci trovammo tutti quanti a Matera per controllare gli allestimenti delle mostre. La sera, stanchi per il lavoro svolto e per il continuo andirivieni da Matera a Metaponto, ci incontrammo tutti insieme a cena in un ristorante nei sassi materani. Durante la cena Tobia mi parlò di una sua osservazione fatta mentre calcolava le radici numeriche, che lui chiamava numeri teosofici, dei numeri primi. Infatti si era accorto che questi non assumevano mai il valore 3, 6 o 9. Di solito le affermazioni sulle regolarità o irregolarità dei primi sono difficili da affrontare e da dimostrare, ma in questo caso la soluzione era abbastanza semplice e Claudio Bertocci la intuì subito. La dimostrazione di questa congettura è conseguenza di un teorema noto anche ai ragazzi delle scuole elementari: il teorema sulla divisibilità di un numero per 3 o 9.  L'osservazione di Tobia aveva messo in risalto una proprietà dei primi, a posteriori abbastanza logica ma a prima vista interessante e sorprendente.

Tobia mi chiese se potevo fargli avere, in modo da pubblicarla nel catalogo di una mostra che stava allestendo a Venezia, una dimostrazione formale del criterio di divisibilità di un numero per 9, 6 o 3.  Intrapresi quindi la dimostrazione della congettura di Tobia, che chiamai seconda congettura di Ravà, in quanto già al nostro primo incontro 12 anni prima, Tobia mi aveva esposto una sua congettura sulla periodicità dei numeri teosofici della sequenza di Fibonacci. Per rendere la dimostrazione più generica mi proposi di dimostrarla per i numeri primi espressi in qualsiasi base numerica e non solo in quella di base 10. Infatti le altre basi numeriche non dovevano subire alcuna discriminazione nelle questioni di teoria dei numeri. La base 10 è una base numerica non ottimale, che deve la sua fortuna unicamente all'atteggiamento antropocentrico di alcune culture antiche, che hanno preferito facilitare il “tener di conto” con le dita della mano invece che rendere più semplice le operazioni di divisione. Infatti la base 12, come quella usata dai babilonesi, e ancora oggi in uso per misurare il tempo, è certamente più efficiente avendo 12 ben 4 divisori e non solamente 2 come 10.

Seconda congettura di Ravà

Le radici digitali, detti anche numeri teosofici, dei numeri primi espressi in base 10 non assumono mai il valore di 3, 6 o 9 in quanto i numeri la cui radice digitale e 3, 6  o 9 hanno per divisore 3 e quindi non possono essere primi

Un numero rappresentato in base 10 con radice digitale 3,6, o 9 è divisibile per 3 per il criterio di divisibilità dimostrato qui in seguito: 

Un numero n può essere rappresentato nel sistema posizionale in base b nel seguente modo:

Sostituendo b_k  con (b_k − 1 + 1)  si ottiene:

          

La 3) rappresenta n parzialmente come somma di fattori moltiplicati per (b^k − 1) che, essendo il numero che precede b^k, è espresso come sequenza ripetuta della cifra più alta della base numerica. Per esempio nel caso della base 10, (b^k − 1)) è rappresentato come (99…9)_k ossia la cifra 9 ripetuta k volte.

Ora 𝑎_k (b^k − 1) è divisibile per (b − 1) in quanto  (b^k − 1) è uguale a  (11…1)_k  * (b − 1)

La somma è quindi sempre divisibile per (b − 1). In base alla 3) n sarà divisibile per (b-1) se ancheè divisibile per  (b − 1) 

Ne consegue che un numero espresso in base dieci è divisibile per 9 se e solo se la sua radice digitale è divisibile per 9.

Qualora (b − 1) sia a sua volta scomponibile in fattori

allora  sarà divisibile anche per qualsiasi dei suoi fattori b_j  e di conseguenza se  è a sua volta divisibile per b_j allora n per la 3) sarà divisibile per b_j

Quindi se la radice digitale di un numero n rappresentato in una base b è uguale a (b − 1), a un fattore b_j di (b − 1)  o a un multiplo di  b_j allora n è un multiplo di  b_j  è quindi non può essere primo. Le radici digitali dei numeri primi possono quindi essere solo numeri che sono coprimi con il numero predecessore della base numerica in cui il primo è rappresentato. Dove per coprimi di un numero si intendono i numeri minori di un numero che non sono fattori o multipli dei fattori del numero stesso.

Nel caso della base 10 se la radice digitale di un numero n è uguale a 9 allora n è divisibile per 9, se invece la radice numerica di n è uguale a 3 o 6 allora n è divisibile per 3. Quindi in questo caso quando la radice digitale di un numero e 3, 6 o 9 allora il numero è divisibile per 3.

Le radici digitali (o numeri teosofici) dei numeri primi espresse in base 10 non saranno quindi mai multipli di 3.

I numeri teosofici dei primi in base 10 non saranno quindi mai 3, 6 o 9.

Qualora i numeri fossero espressi in altre basi le loro radici numeriche non assumerebbero mai il valore della cifra più alta della base o il valore di uno dei suoi fattori o di un multiplo di uno dei fattori qualora questo sia ancora inferiore alla cifra più alta della base.  Le radici numeriche dei primi espressi in una base b possono essere unicamente i coprimi di n dove n = b − 1

In seguito è riportata una tabella delle radici mancati nei primi espressi in diverse basi numeriche. Nel caso della base 2 ogni numero ha per radice digitale il numero 1, infatti tutti i numeri sono divisibile per 1.

	Radici digitali mancanti nei primi	n=(b-1)	Possibili valori della radice digitale nei primi (coprimi di n)	Numero dei coprimi
3	2	2	1	1
4	3	3	1,2	2
5	4,2	4	1,3	2
6	5	5	1,2,3,4	4
7	6,4,3,2	6	1,5	2
8	7	7	1,2,3,4,5,6	6
9	8,6,4,2	8	1,3,5,7	4
10	9,6,3	9	1,2,4,5,7,8	6

Andamento della 𝜑(n) fino a 1000

Mandai la dimostrazione anche a Claudio che mi confermò la correttezza dei ragionamenti facendomi notare che la sequenza che avevo evidenziato era una famosa sequenza numerica molto studiata in teoria dei numeri, la sequenza numerica del numero di coprimi di un numero n chiamata funzione di Eulero 𝜑(n) o toziente.

Questa funzione fu scoperta da Eulero, matematico svizzero, che è considerato il più importante matematico del Settecento, e uno dei massimi della storia. È noto per essere tra i più prolifici di tutti i tempi e ha fornito contributi storicamente cruciali in svariate aree: analisi infinitesimale, funzioni speciali, meccanica razionale, meccanica celeste, teoria dei numeri, teoria dei grafi. Sembra che Pierre Simon Laplace abbia affermato "Leggete Eulero; egli è il maestro di tutti noi".

Eulero dimostrò che la funzione 𝜑(n), che per ogni n indica il numero dei coprimi minori di n di n, può essere espressa anche come

            

Dove p∥n sono tutti e solo i primi che contribuiscono alla fattorizzazione di n.

Eulero partì dalla constatazione che ogni numero per il teorema fondamentale dell’aritmetica può essere espresso come

dove  p_i è un primo fattore di n e r è il numero dei diversi fattori primi di n e quindi per 𝜑(n), vale 

ma la funzione 𝜑(n) di Eulero è moltiplicativa: per ogni coppia di interi 𝑎 e b che siano coprimi, cioè tali che MCD(𝑎, b)=1, si ha:

Ma i valori p_i^k_i essendo potenze di primi sono coprimi tra loro e quindi  

      

in seguito Eulero dimostra che 𝜑(p_i^k_i) può essere espresso come:

            

Infatti i numeri non coprimi di p_i^k_i essendo p_i  primo sono tutti i multipli di p_i  fino a p_i^k_i-1

p_i,  2p_i , 3p_i, ...p_i^k_i-1

Questo insieme ha p_i^k_i-1 membri

Quindi 𝜑(p_i^k_i) il numero dei coprimi di p_i^k_i, sarà dato dalla differenza tra la quantità dei numeri minore o uguale a p_i^k_i cioè  p_i^k_i e la quantità dei numeri non coprimi di p_i^k_i e quindi:

𝜑(p_i^k_i)=p_i^k_i−p_i^k_i-1

Da qui si ottiene la 8)

Ora sostituendo la 8) nella 7) si ottiene

Moltiplicando e dividendo per p_i

Per la proprietà commutativa della moltiplicazione

ma

e quindi

QED

Eulero si pose la domanda quale valore avrebbe assunto il prodottoper tutti gli infiniti numeri primi.

Ora Eulero nel 1737 dimostro che l'inversa di , ovvero  è uguale alla somma della serie armonica:

Ma la serie armonica  diverge e quindi  tende a zero.

Eulero estesa la 9) definendo la funzione ζ(x) , oggi chiamata funzione zeta o prodotto di Eulero.

Dove x e un numero reale maggiore di 1 e dimostrò che

Bernhard Riemann, matematico tedesco, in un articolo pubblicato nel 1859 dal titolo “Über die Anzahl der Primzahlen unter einer gegebenen Größe” estese la funzione zeta di Eulero nel dominio dei numeri complessi e ne studio le caratteristiche. 

La funzione zeta estesa ai numeri complessi, chiamata zeta di Riemann, come risulta dalla 9), ha un polo in Re[1]Im[0]. Inoltre gli zeri della zeta di Riemann sono di due tipi. Gli zeri cosiddetti banali che si trovano tutti sull’asse reale negativo del piano immaginario in corrispondenza dei multipli di Re[-2]Im[0]. Oltre a questi, secondo l’ipotesi formulata da Riemann, la funzione ha zeri non banali che dovrebbero trovarsi tutti sulla retta parallela all’asse imaginario passante per Re[1/2]Im[0].

La dimostrazione o la refutazione dell’ipotesi di Riemann oggi conosciuta come la congettura di Riemann è il problema più importante della teoria dei numeri e forse di tutta la matematica. La soluzione della congettura di Riemann getterebbe luce sulla legge che governa la distribuzione dei numeri primi. Si spera che dalla risoluzione e dalle conseguenze della dimostrazione possa finalmente scaturire una formula che indichi la quantità di primi minori di un numero dato. Chissà che poi questo non apri la strada per trovare il sacro Graal della matematica: la formula che esprima solo e tutti i numeri primi e che quindi squarci il velo che gli avvolge misteriosamente.

Durante le conferenze e le mostre di quel solstizio d’estate materano i numeri primi e la congettura di Riemann furono un argomento ricorrente. Tobia Ravà con la sua osservazione sulle radici numeriche dei numeri primi aveva contribuito forse più di altri alla loro poetica dando pieno senso al nome della manifestazione.