Incontrai Tobia Ravà, artista veneziano, nel marzo del 2007 presso la sua casa, una villa veneta a Mirano, nell’hinterland di Venezia. Lo avevo cercato perché incuriosito da una sua opera raffigurata sulla copertina dei Racconti Matematici a cura di Claudio Bartocci edito da Enaudi, che ritraeva una donna realizzata con numeri e lettere ebraiche. Durante il nostro incontro Tobia mi parlò della tradizione esoterica ebraica, la cabbala, ed in particolare di una metodo di analisi delle scritture chiamato ghematria. Questo metodo sfrutta la proprietà della notazione numerica ebraica che rappresenta i numeri non usando simboli speciali, ma alla pari dei Greci, usa le lettere dell'alfabeto in una notazione additiva. Ogni parola scritta quindi oltre a rappresentare un concetto rappresenta quindi anche un numero. Questo permette lo studio delle parole e dei testi anche dal punto di vista numerologico. Ogni numero associato ad una parola può inoltre essere ridotto ad un unico numero minore di 10 sommandone le cifre ed ottenendo così un numero derivato. Se questo risulta maggiore o uguale di 10 questo processo viene ripetuto fino ottenere un numero ad una solo cifra. Tobia chiamava questo numero “numero teosofico” della parola o del numero di partenza.
In matematica questo processo è definito come la radice digitale di un numero e trova applicazione nei criteri di divisibilità e nella “prova del nove” usata per il controllo della correttezza delle operazioni aritmetiche.
I cabalisti, invece, usavano questi numeri per interpretare le scritture sacre. Secondo loro la struttura numerica della lingua ebraica e delle sacre scritture ne rivela la provenienza divina. Infatti, alcune coincidenze svelano un ordine nascosto nella lingua ebraica. Per esempio Tobia mi fece notare che la somma del numero teosofico della parola “padre” (av 3) e della parola “madre” (em 5) in ebraico risultava uguale al numero teosofico della parola “bambino” (yeled 8).
In matematica questo processo è definito come la radice digitale di un numero e trova applicazione nei criteri di divisibilità e nella “prova del nove” usata per il controllo della correttezza delle operazioni aritmetiche.
I cabalisti, invece, usavano questi numeri per interpretare le scritture sacre. Secondo loro la struttura numerica della lingua ebraica e delle sacre scritture ne rivela la provenienza divina. Infatti, alcune coincidenze svelano un ordine nascosto nella lingua ebraica. Per esempio Tobia mi fece notare che la somma del numero teosofico della parola “padre” (av 3) e della parola “madre” (em 5) in ebraico risultava uguale al numero teosofico della parola “bambino” (yeled 8).
Tobia aveva inoltre uno spiccato interesse per le sequenze numeriche specialmente per la sequenza di Fibonacci. Mi raccontò che aveva scoperto che se calcolava i numeri teosofici della sequenza questi si ripetevano ogni 24 numeri della sequenza. Tobia aveva testardamente verificato la veridicità di questa regolarità della sequenza fino ad indici elevati e supponeva che questa regolarità si potesse protrarre all’infinito. La verifica numerica, anche se protratta per indici molto elevati della sequenza, chiaramente non dimostrava nulla, ma si poteva solo congetturarne la veridicità. Gli promisi di dimostrare la sua congettura in maniera deduttiva al più presto.
Congettura di Ravà
Le radici digitali in base 10 (numeri teosofici) della sequenza di Fibonacci sono una sequenza periodica con periodo 24.
In realtà la congettura vale non solo per la base 10 ma per tutte le basi numeriche possibili, anche se in basi diverse la successione delle cifre si ripete con periodi diversi.. Affronteremo quindi la dimostrazione per una base qualsiasi b.
In realtà la congettura vale non solo per la base 10 ma per tutte le basi numeriche possibili, anche se in basi diverse la successione delle cifre si ripete con periodi diversi.. Affronteremo quindi la dimostrazione per una base qualsiasi b.
Definizione di radice digitale
La radice digitale dr di un intero n si ottiene con un processo costituito da successivi k passi riduttivi ciascuno dei quali consiste nel ricavare da un intero la somma delle sue cifre nella notazione in base b.
n è rappresentato nella base b come
la sua radice digitale è ottenuta il ripetendo la somma
fino a che nk+p è rappresentato nel sistema a base b con una sola cifra.
il numero delle iterazioni p è chiamato persistenza additiva.
Chiameremo la radice digitale in base 10 di un numero il valore teosofico del numero.
La radice digitale di un intero n può essere calcolata usando la funzione modulo. Infatti il valore teosofico può anche essere calcolato come (n) mod (b-1) che rappresenta il resto della divisone di n per (b-1). Nel caso della base 10 il numero teosofico può essere quindi calcolato anche come resto della divisione per 9.

ovvero in forma compatta

ovvero in forma compatta
la (1.4) si può dimostrare a partire dalle proprietà additive e associative della funzione modulo.
infatti applicando la funzione modulo alla (1.1) per la proprietà additiva (1.3)
e quindi la (1.8)
ma (bk) mod (b-1)=1 per ogni k e quindi
da cui si ricava la (1.4)
la seconda parte della (1.4) altro non è che il criterio di divisibilità per (b-1) dove b e la base della notazione numerica.
La radice digitale gode della proprietà additiva per cui la radice digitale dr della somma di due interi n e m è uguale alla radice digitale delle somme delle radici digitali degli addendi.

e quindi
%5C+dr(dr(n)+dr(m))=dr(n+m))
Successione di Fibonacci
1,2,3,5,8,13,21,34,55,89......
Proprietà delle radici digitali della sequenza di Fibonacci
%5C+dr(F_%7Bn%7D)=dr(dr(F_%7Bn-1%7D)+dr(F_%7Bn-2%7D)))

e quindi
Successione di Fibonacci
La successione di Fibonacci è una successione di numeri interi naturali definibile assegnando i valori dei due primi termini, F0=0 ed F1=1, e chiedendo che per ogni termine successivo sia Fn=Fn-1 + Fn-2 con n>1. Il termine F0 viene aggiunto nel caso si voglia fare iniziare la successione con 0; storicamente il primo termine della successione è F1= 1.
1,2,3,5,8,13,21,34,55,89......
Ogni elemento della sequenza di Fibonacci è somma dei due predecessori e quindi in base alla (1.9) la radice digitale di un elemento della sequenza di Fibonacci è la radice digitale delle somme delle radici digitali dei due predecessori della sequenza di Fibonacci.
Dimostrazione della congettura
Chiamammo successione di Fibonacci radicale la sequenza delle radici digitali della sequenza di Fibonacci. Questa sequenza, in base alla (1.10), è una successione di Fibonacci nel Gruppo ℤ(0..b-1) formato dall’insieme degli interi {0,1,2,.. b-1} associato all’operazione binaria della radice digitale.
Se in questa sequenza ricompaiano ad un certo punto due elementi successivi nello stesso ordine e valore la sequenza diventa periodica.
Visto che la sequenza di Fibonacci radicale è composta da numeri ad una sola cifra, diversi da zero ad eccezione di F0, al più tardi dopo (b-1)2 passi la sequenza diventa periodica essendo (b-1)2 il numero massimo delle possibili combinazioni di due numeri scelti in {1,2,.. b-1}. Infatti, dopo al massimo (b-1)2 passi tutte le possibile coppie di numeri consecutivi si saranno esaurite e quindi la prossima coppia dovrà essere una coppia già comparsa nella sequenza. Da questo punto in poi la sequenza si riproporrà in maniera periodica.
Qed.
La ripetizione di una coppia avviene di solito prima di (b-1)2 passi.
La sequenza di Fibonacci radicale di base 10 è detta sequenza di Fibonacci teosofica.
Nel caso della sequenza di Fibonacci teosofica la ripetizione di due elementi uguali avviene dopo 24 passi.
Le sequenze di Fibonacci radicali per le basi da 2 a 10 sono rappresentate nella tabella seguente
base
|
sequenza
|
periodo
|
2
|
1
|
1
|
3
|
1,2,1
|
3
|
4
|
1,2,3,2,2,1,3,1
|
8
|
5
|
1,2,3,1,4,1
|
6
|
6
|
1,2,3,5,3,3,1,4,5,4,4,3,2,5,2,2,4,1,5,1
|
20
|
7
|
1,2,3,5,2,1,3,4,1,5,6,5,5,4,3,1,4,5,3,2,5,1,6,1
|
24
|
8
|
1,2,3,5,1,6,7,6,6,5,4,2,6,1,7,1
|
16
|
9
|
1,2,3,5,8,5,5,2,7,1,8,1
|
12
|
10
|
1,2,3,5,8,4,3,7,1,8,9,8,8,7,6,4,1,5,6,2,8,1,9,1
|
24
|


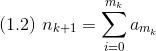
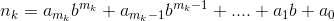




Nessun commento:
Posta un commento