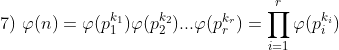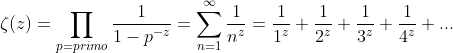La facciata della MiCROTEC: variazioni sugli esagoni di Escher

L'artista olandese Maurits Cornelis Escher intraprese nel 1922, dopo aver concluso gli studi alla scuola di arti grafiche a Haarlem, sulla scia di molti giovani artisti dell’Europa continentale, il Gran Tour in Italia alla ricerca delle radici della cultura occidentale. Rimase talmente affascinato dal paesaggio italiano che decise di stabilirsi a Roma e diventare un artista paesaggista. Ogni primavera intraprendeva viaggi nelle provincie italiane, eseguendo disegni e schizzi di villaggi e paesaggi. Tornato a Roma li trasformava in opere grafiche, inizialmente xilografie, in seguito anche litografie e mezzetinte. Ogni tanto si cimentava anche in opere geometriche più astratte e, molto probabilmente per economizzare lo sforzo dovuto all’incisione sulla matrice lignea, aveva sviluppato una tecnica per realizzare, usando un unico tassello, opere più complesse stampando il tassello l’uno accanto all’altro: in tal modo il piano veniva riempito con figure uguali, ma usando colori e orientazioni diverse veniva a crearsi un insieme in cui la monotona regolarità della ripetizione era mitigata e impreziosita dall’alternarsi dei colori e delle orientazioni. Le possibili operazioni su un tassello nel tentativo di riempire il piano con la stessa figura sono, oltre naturalmente all’essenziale traslazione, la rotazione e la riflessione.  

Figura 1 Sciarpa in seta stampata a mano 1925

Figura 2 Tasselli per la stampa della sciarpa 

Mentre la rotazione era banalmente eseguita ruotando il tassello matrice, la riflessione richiede la costruzione di una seconda matrice con la figura speculare (figura 2). M.C. Escher si cimentò, durante la sua permanenza a Roma, in diversi tipi di tassellature stampando motivi regolari su tessuti, oltre a cimentarsi nel disegno delle piastrelle di ceramica usate per pavimentare la sua casa romana (figura 3). Nel 1936 Escher, a causa dell’inasprirsi della situazione politica e infastidito dalla propaganda nazionalista del regime fascista, abbandonò l’Italia per trasferirsi a Chateaux d’Aux in Svizzera. Ma la nostalgia per il paesaggio italiano, soprattutto per quello dell’Italia meridionale, lo spinse a intraprendere un ultimo viaggio per imprimere definitamente nella memoria le stratificazioni culturali e le diversità del paesaggio mediterraneo. Scrisse alla compagnia di navigazione Adria di Fiume, chiedendo di potersi imbarcare su una motonave che percorresse le rotte del Mediterraneo in cambio di 48 stampe risultanti dalle incisioni basate sui disegni eseguiti durante il viaggio.

Figura 3 Disegno per le piastrelle della casa in via Poerio a Roma

 

La compagnia di navigazione Adria accettò e quindi Escher si imbarcò il 27 Aprile 1936 sulla motonave Rossini. Il viaggio lo portò a toccare tanti porti del Mediterraneo, ma fu a Granada in Spagna che avvenne quello che mise definitivamente in secondo piano l’interesse di Escher per il paesaggio. Escher a Granada visitò l’Alhambra, la fortezza costruita dai mori nel 13mo secolo, durante il loro dominio sulla penisola Iberica. I mori per abbellire le loro dimore, dovendo seguire il precetto musulmano della proibizione della rappresentazione di figure animate, ricorrevano a ornamenti geometrici. Molto probabilmente, per le stesse ragioni di economia che avevano indotto Escher a usare una sola matrice per creare pattern più complessi, le pareti dell’Alhambra erano piastrellate con tasselli di ceramica che si ripetevano secondo diversi schemi simmetrici. La varietà degli schemi incuriosì Escher che fece molti schizzi delle diverse simmetrie (Figura 4).  

 

Figura 4 Disegno delle decorazioni murali dell’Alhambra eseguite da M.C. Escher nel 1936

Tornato a Chateau d’Aux, iniziò a studiare intensamente le diverse simmetrie che permettevano di tassellare il piano. Gli venne in aiuto il fratellastro Beer[1] , un insigne geologo che insegnava all’Università di Leida . Gli interessi scientifici di Beer Escher erano rivolti soprattutto alla vulcanologia, ma anche la cristallografia era tra i suoi campi d’interesse. I cristallografi, nell’intento di classificare tutti i tipi di cristalli, si erano cimentati nell’approcciare il problema con le tecniche della matematica. Il problema dei cristallografi era equivalente al problema della tassellatura. Infatti i cristalli sono composti da celle che ripetute formano il reticolo cristallino. Anche qui le trasformazioni possibili sono, oltre alle traslazioni, le rotazioni e le riflessioni, solo che invece di svilupparsi sul piano le trasformazioni si sviluppano nello spazio. I cristallografi, nell’intento di capire con quali metodi affrontare il problema dei cristalli nello spazio tridimensionale[2],  affrontarono anche il problema più semplice, cercando di capire come le trasformazioni generano tutte le possibili tassellature del piano. Le trasformazioni che lasciano invariate la forma e le dimensioni di enti geometrici sono studiate dalla teoria dei gruppi e sono chiamate trasformazioni isometriche. Le operazioni isometriche, traslazioni, rotazioni e riflessioni, definisco un ‘gruppo’. La teoria dei gruppi era stata sviluppata da Evariste Galois[3] negli anni ‘30 del 19mo secolo allo scopo di determinare la solubilità delle equazioni polinomiali. Applicando le tecniche della teoria dei gruppi i cristallografi Fedorov, Schoenflies e Barlow nel 1891 avevano dimostrato che i differenti gruppi di trasformazioni atti a riempire una superficie piana con figure regolari sono in tutto 17. I gruppi delle isometrie del piano sono spesso chiamati “wallpaper group”, gruppo della carta da parati. Infatti, la carta da parati è il più delle volte decorata con disegni simmetrici tali da non evidenziare il passaggio da un foglio all’altro, in modo da dare alla parete una decorazione senza interruzione di continuità.

Escher era venuto a conoscenza attraverso il fratellastro di un articolo di Pólya[4]  del 1924 in cui le 17 possibilità erano state riscoperte e illustrate. Escher aveva poi spinto oltre la sua indagine (figura 5) considerando anche il colore come elemento distintivo (tasselli adiacenti non potevano condividere lo stesso colore) e catalogò in un suo originale schema le diverse possibilità sviluppando una vera e propria teoria[5].

Figura 5 Tassellazioni con simmetrie identiche (traslazione e riflessione) ma che non possono essere colorate secondo lo stesso schema 

Nel 1939, in seguito allo scoppio della seconda guerra mondiale, M.C. Escher si stabilì a Baarn, nella natia Olanda. Aveva passato gli ultimi anni studiando a fondo le isometrie del piano e aveva raccolto in un quaderno esempi di diverse tassellature. Le tassellature di Escher avevano una particolarità che prima di lui nessun altro aveva sistematicamente sviluppato[6]. Le sue erano tassellature animate: i suoi tasselli non erano semplici figure geometriche, ma avevano forma e soggetti riconoscibili come uccelli, pesci, rettili.  Escher continuò a studiare le diverse tipologie di figure geometriche che avevano la proprietà di tassellare il piano. Nel 1937 il fratellastro Beer gli fece avere un articolo del cristallografo tedesco F. Haag[7] che descrive le proprietà di un particolare esagono costruito partendo da un triangolo equilatero e da un punto qualsiasi sul piano. Haag costruiva un primo lato dell’esagono congiungendo il punto F (un punto qualsiasi) con un vertice del triangolo equilatero, il punto A (Figura 6). Il secondo lato è costruito ruotando il primo di 120˚ intorno al vertice A del triangolo equilatero, quindi congiungendo l’estremo del secondo lato, il punto D, con il successivo vertice del triangolo equilatero, il punto B, seguendo il verso della rotazione e ripetendo la costruzione anche per l’ultimo vertice. Haag dimostrò che si formava un esagono e che questo esagono, proprio perché costruito sul reticolo dei triangoli equilateri, tassellava il piano. 

Escher studiando gli esagoni di Haag, che in seguito chiameremo esagoni di Escher, notò che tracciando le diagonali queste si incontravano in un solo punto. Escher enunciò il suo risultato alla maniera formale dei matematici in forma di enunciato di un teorema (figura 7). Infatti, nell’enunciarlo usò il termine “stelling” la parola olandese per definire la tesi di un teorema. L’enunciato di Escher era corretto, anche se l’artista ne aveva solo verificato la validità per via grafica, testando la sua tesi su diversi esagoni e, da abile disegnatore, notando che le diagonali si incontravano sempre in un unico punto. 

Figura 6 Esagoni di Escher

Una dimostrazione matematica rigorosa, che si riferiva ad un caso più generale, era stata pubblicata nel 1825 da Karl Friedrich Andreas Jacobi[8] un matematico tedesco da non confondere con il più famoso Carl Gustav Jacobi. Nel 1973 J.F. Rigby presentò una dimostrazione[9] che si basava sulle simmetrie di rotazione e di traslazioni della tassellatura di Haag. Questa dimostrazione, essendo basata sulla proprietà dell’esagono di tassellare il piano, sarebbe certamente piaciuta da Escher. 

Figura 7 M.C. Escher Appunti

Figura 8 Teorema di Napoleone

Escher non era a conoscenza del lavoro di Jacobi e chiese a suo figlio George una dimostrazione. George si era laureato in ingegneria e intratteneva con il padre una fitta corrispondenza riguardo alle questioni matematiche sulle tassellature del piano. George Escher non riuscì ad accontentare il padre, ma osservò che gli esagoni di Escher, potevano essere costruiti anche in maniera differente. George fece notare al padre che i segmenti che sottendono gli angoli di 120˚ formati dai lati uguali dell’esagono di Escher definiscono un triangolo DEF e che i triangoli isosceli con vertice di 120˚, ruotati di +/- 120˚, formano triangoli equilateri costruiti sui lati del triangolo DEF. Inoltre, i centri di tali triangoli equilateri sono precisamente i vertici del triangolo equilatero iniziale ABC a partire dal quale, partendo dal punto F preso arbitrariamente, era stato costruito l’esagono di Escher.  Pertanto, l’esagono di Escher ADBECF può anche essere costruito a partire da un triangolo qualsiasi DEF, costruendo sui suoi lati dei triangoli equilateri i cui centri A, B, C   sono a loro volta vertici di un triangolo equilatero. Questo risultato era conosciuto in geometria come il teorema di Napoleone.

Il teorema di Escher quindi era intimamente connesso attraverso gli esagoni a un altro teorema della geometria del triangolo che la tradizione attribuisce appunto a Napoleone Buonaparte[10], il quale, oltre ad essere un grande condottiero, era un valente matematico dilettante. La connessione è sorprendente anche in virtù del fatto che sia Escher che Napoleone erano appunto matematici dilettanti. Escher si rese certamente conto che i suoi esagoni, costruiti su un reticolo di triangoli equilateri, individuavano i triangoli di Napoleone, iscritti a loro volta in nuovi esagoni (non congruenti) determinati dai vertici dei triangoli di Napoleone e dai punti di incontro delle diagonali degli esagoni di Escher.  

Figura 9 M.C Escher, Divisione regolare del piano Nr 10, Acquarello 1942

Infatti, Escher nel maggio del 1942 disegna una tassellatura del piano (figura 9) nella quale sono chiaramente individuabili le diagonali degli esagoni di Escher e i triangoli di Napoleone. Ma c’è un altro sorprendente aspetto nella pavimentazione di Escher che la collega a nomi di illustri matematici del XVII secolo. Indicati. infatti con A’, B’, C’ gli ulteriori vertici dei triangoli di Napoleone aventi come centri rispettivamente i punti A, B, C, anche gli esagoni A’DB’EC’F godono della proprietà che le loro diagonali si intersecano in un unico punto PF: ebbene, tale punto risulta essere, nel caso in cui il triangolo DEF non contenga angoli di ampiezza maggiore di 120°[11], il punto di minima distanza dai vertici di tale triangolo. Il punto PF è noto come punto di Fermat, in quanto fu proprio Pierre de Fermat ad individuarlo in risposta a un quesito posto da Evangelista Torricelli che diede luogo a una fitta corrispondenza tra i due grandi matematici.  La concorrenza delle diagonali cosi costruite nel punto di Fermat è conseguenza dello stesso teorema di Jacobi del 1825. Inoltre nel 1870 Ludwig Kiepert dimostrò che il punto individuato da Escher ed il punto d Fermat giacevano su una iperbole equilatera che passa anche per i tre vertici del triangolo di partenza, il suo ortocentro ed il suo baricentro[12]

Escher esegue anche un altro acquarello (figura 11) basato sugli esagoni di Escher, sovrapponendo quattro reticoli costruiti con tali esagoni.  Al primo reticolo vengono sovrapposti gli altri tre traslati lungo tre vettori U2, V2, W2 (figura 13) che muovono il reticolo di metà del percorso che traslerebbero secondo i vettori U1, V1, W1,  ognuno dei quali trasforma il reticolo in sé stesso. Sul reticolo combinato si individua un nuovo punto concorrente. J.F. Rigby nel suo articolo del 1973 dimostra che questo punto è il centro del cerchio dei nove punti del triangolo DEF. Questo cerchio chiamato anche cerchio di Feuerbach[13], contiene infatti oltre ai punti medi dei lati del triangolo DEF anche i piedi delle sue altezze e i punti medi dei segmenti compresi fra i vertici e l'ortocentro.

Figura 10 Punto di Fermat

A ogni esagono di Escher è associato, come aveva fatto notare il figlio George, un triangolo e le proprietà dell’esagono sono intimamente, e anche sorprendentemente, connesse con quelle dei triangoli. Ma le sorprese non sono finite. Infatti l’osservazione di Escher sulla concorrenza delle diagonali dell’esagono di Escher implica in base al teorema di Brianchon , che gli esagoni di Escher iscrivono un’ellisse[14]. Il teorema Brianchon afferma che, date sei rette tangenti a una conica che si intersecano a due a due in sei punti, le rette che congiungono i punti opposti si incontrano in un punto. Il teorema ha come corollario che per un esagono circoscritto a una conica le rette congiungenti vertici opposti passano per uno stesso punto, detto punto di Brianchon.

Il teorema vale anche nella sua versione inversa. Se le diagonali di un esagono si incontrano in un punto, è possibile iscrivere un’ellisse che è tangente a tutti i sei lati.

Figura 11 M.C Escher, Divisione regolare del piano, Nr 11 Acquarello 1942

Gli esagoni di Escher e la proprietà delle diagonali individuata da Escher mettono in evidenza tutta una serie di risultati della geometria piana e, in particolare, della geometria del triangolo che vanno molto oltre la trattazione fatta da Euclide nel 300 a.C. nei suoi Elementi e che fanno intravedere la ricchezza e la complessità delle questioni legate a costruzioni geometriche apparentemente semplici.  

 

Figura 12 U1, V1, W1 i tre vettori di traslazione che trasformano il reticolo in sé stesso

Per celebrare il genio olandese la ditta MiCROTEC di Bressanone ha voluto costruire la facciata della nuova sede ispirandosi alla tassellatura generata dalle diagonali degli esagoni di Escher, integrata qua e là dai triangoli di Napoleone. La tassellatura si prestava per essere costruita in modo modulare. Infatti tutto il reticolo poteva essere costruito a partire da un unico elemento a Y il quale opportunamente ruotato ed inserito nel sottostante reticolo dei triangoli equilateri generava tutta la struttura. Questa proprietà, che ha decisamente semplificato la costruzione della facciata, è stata notata dall’architetto Richard Hassell[16] dello studio WOHA di Singapore. Richard Hassell, oltre ad essere un esperto e collezionista delle opere di M.C. Escher, è a sua volta un abile tassellatore,  specializzato nelle tassellature aperiodiche scoperte da Roger Penrose nel 1972.  

Figura 13 Facciata della sede della MiCROTEC in Via Julius Durst 98, 39042 Bressanone, BZ, Italia

Per rendere la facciata più dinamica l’architetto Elisabetta Ripamonti dello studio MMdesign di Milano ha introdotto una variante ispirata alle tassellature metamorfiche di Escher. Infatti molte delle opere di Escher sono costruite modificando i tasselli in modo da passare da una tassellatura ad un’altra. L’esempio più conosciuto è la serie delle tre xilografie Metamorphose[17] considerate da molti come le opere più importanti dell’artista olandese. 

Figura 14 M.C. Escher, Metamorphose II, xilografia a due colori, 1940 didascalia

Nel caso della facciata la metamorfosi è generata come variazione su tre diversi esagoni di Escher, costruiti sullo stesso reticolo di triangoli, ma modificando il punto arbitrario di partenza in modo da generare tre diversi reticoli di esagoni di Escher sul quale poi costruire il reticolo finale unicamente con le semi-diagonali. 

Per richiamare il logo della MiCROTEC i triangoli di Napoleone e il reticolo sono realizzati nei colori del corporate design dell’azienda. Un set completo di triangoli di Napoleone è realizzato in rosso per richiamare il caratteristico punto rosso sulla i del logo MiCROTEC. 

Escher in alcune delle sue opere metteva in evidenza il principio generatore alla base dell’opera[17]. In questo senso il set completo dei triangoli di Napoleone che individuano il triangolo di partenza, evidenziati in rosso, vuole anche essere un riferimento al principio generatore dell’intera struttura.

Il progetto esecutivo è stato realizzato dall’architetto Marco Sari di Treviso e la costruzione realizzata dalla ditta LignoAlp di Bressanone nel periodo da luglio a settembre del 2020. La nuova sede della MiCROTEC è stata inaugurata in occasione del 40mo anniversario dell’azienda il 25 Settembre del 2020. Oltre alle persone già citate vorrei ringraziare anche Mark Veldhuysen e il Gemeentemuseum di den Haag per aver messo a disposizione i loro archivi per la documentazione iconografica. Un particolare ringraziamento va a Piergiorgio Odifreddi per le lunghe chiacchierate sull’argomento e a Doris Schnattschneider e Luigi Grasselli per il loro supporto da matematici professionisti.  Vorrei ringraziare inoltre Alex Terzariol di MMDesign per il contributo alla ideazione e Nicola Cella della MiCROTEC per il coordinamento dei fornitori e della messa in opera.

L’arte di M.C. Escher mi ha accompagnato lungo il percorso della mia vita a partire dall’adolescenza. La sua arte ed in particolare la tassellazione del piano, come metafora della struttura quantizzata dell’universo, mi ha sempre affascinato[18]. La tassellazione con gli esagoni di Escher si presta più di altre a questa metafora: la griglia degli esagoni a rappresentare lo spazio quantizzato e i triangoli, le particelle subatomiche indivisibili[19]. 

Studiare, analizzare, contemplare queste strutture mi aiuta a superare il malessere esistenziale derivante dalle dicotomie del continuo e dell’infinito e quindi ad accettare con convinzione il discreto e il finito. 

L’ultimo ringraziamento va quindi al maestro: Grazie Maurits! 

Note:

[1] Berend George Escher, https://en.wikipedia.org/wiki/Berend_George_Escher, Wikipedia 2020

[2] il numero delle possibili tassellature dello spazio con solidi soggetti a isometrie è limitato, 230, per la precisione. Ciò fu dimostrato dal cristallografo Evgraf S. Fedorov nel 1890.

[3] Évariste Galois (Bourg-la-Reine, 25 ottobre 1811 – Parigi, 31 maggio 1832) è stato un matematico francese. Ancora adolescente, fu in grado di determinare una condizione necessaria e sufficiente affinché un polinomio sia risolubile per radicali, risolvendo quindi un problema vecchio di oltre 350 anni. I suoi lavori hanno portato alla nascita della teoria di Galois e della teoria dei gruppi, due importanti branche dell'algebra astratta. Morì all'età di 20 anni, a causa delle ferite riportate in un duello.

[4] George Pólya (13 dicembre 1887-7 settembre 1985) era un matematico ungherese. È stato professore di matematica dal 1914 al 1940 all'ETH di Zurigo e dal 1940 al 1953 alla Stanford University.

[5] Doris Schattenschneider, Visions of Symmetry, Revised edition published by W. Freeman, 1990

[6] Prima di Escher Koloman Moser (1869 – 1918) esponente della Secessione Viennese in più riprese pubblicò sulla rivista Ver Sacrum tassellature periodiche basate su figure che rappresentavano elementi naturali destinati a essere usati 

[7] Friedrich Haag, Die regelmäßigen Planteilungen und Punktsysteme, Zeitschrift für Kristallographie, Volume 58, 1923, pp. 478–489

[8] Karl Friedrich Jacobi, De triangulorum rectilineorum proprietatibus quibusdam nondum satis cognitis, Typis Klaffenbachii, 1825 decori per carta da parati.

[9] J.F. Rigby, Napoleon, Escher and Tesselations, Mathematics Magazine 64, 1991, pp 242-246

[10] Tale teorema è stato attribuito a Napoleone Bonaparte probabilmente più per riconoscergli un certo interesse nei riguardi della geometria che per merito della scoperta. Di certo è che Napoleone, sulla scia della Rivoluzione Francese, fondò o rifondò delle eccellenti scuole tecniche quali l'École Normale e l'École Polytechnique, scuole dove tenevano lezione i maggiori matematici del tempo quali Lagrange, Laplace, Monge, e che contribuirono non poco allo sviluppo e alla diffusione della matematica

[11] in caso contrario il punto di minima distanza è il vertice dell’angolo maggiore di 120°

[12] Federico Giudiceandrea, Luigi Grasselli, From M. C. Escher’s Hexagonal Tiling to the Kiepert Hyperbola, Journal for Geometry and Graphics Volume 25 (2021), No. 1, 79–95 

[13] Nella geometria piana, consideriamo un triangolo ABC e i punti medi A', B' e C' dei suoi lati. Il cerchio che passa per i punti A', B' e C' prende il nome di cerchio di Feuerbach. Questo nome ricorda il suo scopritore, il matematico tedesco Karl Feuerbach (1800-1834). Il centro del cerchio di Feuerbach giace sulla retta che contiene l'ortocentro, il baricentro e il circocentro, ossia sulla retta di Eulero del triangolo ABC.

[14] Un’ellisse, avendo 5 gradi di libertà, è unicamente determinata da 5 punti oppure 5 tangenti. A causa di questa caratteristica non ogni esagono iscrive al suo interno un’ellisse e quindi questa particolarità caratterizza ulteriormente il sottoinsieme degli esagoni di Escher rispetto all’insieme di tutti gli esagoni.

[15] https://www.richardhassell.net/

[16] Metamorphosis II è una xilografia creata ad M.C Escher, tra il novembre 1939 e il marzo 1940. Questa stampa misura 19,2 per 389,5 centimetri ed è stata stampata da 20 blocchi su 3 fogli combinati. Escher ha anche realizzato una versione più corta (90,7 cm) nel 1937: Metamorphosis I e una più lunga (680 cm) nel 1968: Metamorphosis III

[17] Per esempio nelle opere di M.C. Escher Belvedere (1958) e Concavo e Convesso (1955) sono presenti riferimenti all’illusione ottica presente nel quadro.

[18] La teoria dei gruppi che governa le tassellature del piano è anche alla base della fisica delle particelle elementari. In particolare il Modello Standard è una teoria che descrive insieme tre delle quattro forze fondamentali, cioè l’interazione nucleare forte, l’elettromagnetismo e l’interazione nucleare debole (queste ultime due unificate nell’interazione elettrodebole), nonché la funzione e le proprietà di tutte le particelle (note ed osservate) che costituiscono la materia. Si tratta di una teoria di campo quantistica, coerente sia con la meccanica quantistica che con la relatività speciale. Il comportamento delle particelle può essere descritto complessivamente in modo generale ed esatto usando un gruppo unitario chiamato gruppo di Gauge. 

[19] Il Modello Standard non considera i gravitoni, cioè le particelle che si pensa debbano mediare l’interazione gravitazionale. Le teorie che tentano di unificare il Modello Standard con relatività generale e quindi tengono conto della gravità, dette teorie del tutto, sono diverse e attendono di essere verificate sperimentalmente. Una cosa però le accomuna tutte: la quantizzazione dello spazio stesso. Questo implica che lo spazio che ci circonda non è divisibile all’infinito ma è quantizzato, composto di “a-tomi” di spazio indivisibili. Questi atomi riempiono lo spazio, senza lasciare “spazi vuoti” fra di loro.

La poetica dei numeri primi

La poetica dei numeri primi

Nel 2019 Matera è stata capitale europea della cultura. Il comitato organizzatore della manifestazione incaricò Piergiorgio Odifreddi di organizzare alcuni eventi di natura matematica inseriti in un progetto dal nome accattivante di “la poetica dei numeri primi”. Il progetto si sviluppava in due diversi sedi, Matera e Metaponto e doveva attraverso linguaggi diversi, quello della divulgazione e quello dell’arte, riproporre l’eredità intellettuale di Pitagora che proprio a Metaponto aveva trovato il suo ultimo riposo. Tra gli ospiti erano previsti, tra gli altri, il premio Nobel per la letteratura John Coetzee, scienziati del valore di Guido Tonelli e Ian Stewart e il più noto divulgatore italiano Pietro Angela. Era prevista anche una sezione dedicata all’arte ispirata alla matematica e Piergiorgio mi chiese di allestire una mostra sull’arte delle tassellazioni, l'uso di tasselli regolari, geometrici o dalla forma animata, per riempire il piano senza lasciare spazi vuoti. In particolare la mostra doveva, oltre a illustrare la teoria alla base della tassellazione regolare, esporre opere di artisti che si erano cimentati in questa difficile arte ed in particolar modo le opere dell’indiscusso maestro di questa disciplina: M.C Escher. Oltre alla mostra sulle tassellazioni, nella sezione dedicata all’arte erano previste altre mostre dedicate ad artisti che si erano ispirati alla matematica. Era prevista una mostra di Ugo Nespolo, una retrospettiva di Aldo Spizzichino e una mostra dell’artista veneziano Tobia Ravà, che per l’occasione aveva preparato la mostra “Elementi di calcolo trascendentale”. Conoscevo l’arte di Tobia basata sulla tradizione esoterica ebraica, la cabbala, ed in particolare sul metodo di analisi delle scritture chiamato ghematria. Questo metodo sfrutta la proprietà della notazione numerica ebraica, che rappresenta i numeri, senza usare simboli speciali ma con le lettere dell'alfabeto in una notazione additiva. Ogni parola scritta quindi oltre a rappresentare un concetto rappresenta quindi anche un numero. Questo permette lo studio delle parole e dei testi anche dal punto di vista numerologico. Ogni numero associato ad una parola può inoltre essere ridotto ad un unico numero minore di 10 sommando ripetutamente le cifre fino ottenere un numero ad una sola cifra. In matematica questo processo definisce la radice numerica di un numero. Tobia, con una tecnica divisionista, usava i numeri per formare le figure e visto che ai numeri corrispondevano parole e concetti, questi non erano disposti a caso, ma definivano percorsi descrittivi che formavano un ulteriore strato interpretativo dell'opera.

Partecipava alla manifestazione anche Claudio Bartocci docente di fisica matematica e storia della matematica all'università d Genova, che aveva per l’occasione insieme a Luigi Civalleri allestito la mostra dal titolo: “Numeri nel tempo. Contare, misurare, calcolare”. Era stato Claudio a farmi conoscere 12 anni fa Tobia, infatti sul frontespizio di una antologia di racconti matematici del edita da Enaudi nel 2006 e da lui curata, era raffigurata il volto di una donna realizzato da Tobia con numeri colorati. Incuriosito dall’uso dei numeri per raffigurare figure mi misi in contatto con Tobia, diventando in seguito un estimatore della sua particolare arte.

Il giorno prima del solstizio ci trovammo tutti quanti a Matera per controllare gli allestimenti delle mostre. La sera, stanchi per il lavoro svolto e per il continuo andirivieni da Matera a Metaponto, ci incontrammo tutti insieme a cena in un ristorante nei sassi materani. Durante la cena Tobia mi parlò di una sua osservazione fatta mentre calcolava le radici numeriche, che lui chiamava numeri teosofici, dei numeri primi. Infatti si era accorto che questi non assumevano mai il valore 3, 6 o 9. Di solito le affermazioni sulle regolarità o irregolarità dei primi sono difficili da affrontare e da dimostrare, ma in questo caso la soluzione era abbastanza semplice e Claudio Bertocci la intuì subito. La dimostrazione di questa congettura è conseguenza di un teorema noto anche ai ragazzi delle scuole elementari: il teorema sulla divisibilità di un numero per 3 o 9.  L'osservazione di Tobia aveva messo in risalto una proprietà dei primi, a posteriori abbastanza logica ma a prima vista interessante e sorprendente.

Tobia mi chiese se potevo fargli avere, in modo da pubblicarla nel catalogo di una mostra che stava allestendo a Venezia, una dimostrazione formale del criterio di divisibilità di un numero per 9, 6 o 3.  Intrapresi quindi la dimostrazione della congettura di Tobia, che chiamai seconda congettura di Ravà, in quanto già al nostro primo incontro 12 anni prima, Tobia mi aveva esposto una sua congettura sulla periodicità dei numeri teosofici della sequenza di Fibonacci. Per rendere la dimostrazione più generica mi proposi di dimostrarla per i numeri primi espressi in qualsiasi base numerica e non solo in quella di base 10. Infatti le altre basi numeriche non dovevano subire alcuna discriminazione nelle questioni di teoria dei numeri. La base 10 è una base numerica non ottimale, che deve la sua fortuna unicamente all'atteggiamento antropocentrico di alcune culture antiche, che hanno preferito facilitare il “tener di conto” con le dita della mano invece che rendere più semplice le operazioni di divisione. Infatti la base 12, come quella usata dai babilonesi, e ancora oggi in uso per misurare il tempo, è certamente più efficiente avendo 12 ben 4 divisori e non solamente 2 come 10.

Seconda congettura di Ravà

Le radici digitali, detti anche numeri teosofici, dei numeri primi espressi in base 10 non assumono mai il valore di 3, 6 o 9 in quanto i numeri la cui radice digitale e 3, 6  o 9 hanno per divisore 3 e quindi non possono essere primi

Un numero rappresentato in base 10 con radice digitale 3,6, o 9 è divisibile per 3 per il criterio di divisibilità dimostrato qui in seguito: 

Un numero n può essere rappresentato nel sistema posizionale in base b nel seguente modo:

Sostituendo b_k  con (b_k − 1 + 1)  si ottiene:

          

La 3) rappresenta n parzialmente come somma di fattori moltiplicati per (b^k − 1) che, essendo il numero che precede b^k, è espresso come sequenza ripetuta della cifra più alta della base numerica. Per esempio nel caso della base 10, (b^k − 1)) è rappresentato come (99…9)_k ossia la cifra 9 ripetuta k volte.

Ora 𝑎_k (b^k − 1) è divisibile per (b − 1) in quanto  (b^k − 1) è uguale a  (11…1)_k  * (b − 1)

La somma è quindi sempre divisibile per (b − 1). In base alla 3) n sarà divisibile per (b-1) se ancheè divisibile per  (b − 1) 

Ne consegue che un numero espresso in base dieci è divisibile per 9 se e solo se la sua radice digitale è divisibile per 9.

Qualora (b − 1) sia a sua volta scomponibile in fattori

allora  sarà divisibile anche per qualsiasi dei suoi fattori b_j  e di conseguenza se  è a sua volta divisibile per b_j allora n per la 3) sarà divisibile per b_j

Quindi se la radice digitale di un numero n rappresentato in una base b è uguale a (b − 1), a un fattore b_j di (b − 1)  o a un multiplo di  b_j allora n è un multiplo di  b_j  è quindi non può essere primo. Le radici digitali dei numeri primi possono quindi essere solo numeri che sono coprimi con il numero predecessore della base numerica in cui il primo è rappresentato. Dove per coprimi di un numero si intendono i numeri minori di un numero che non sono fattori o multipli dei fattori del numero stesso.

Nel caso della base 10 se la radice digitale di un numero n è uguale a 9 allora n è divisibile per 9, se invece la radice numerica di n è uguale a 3 o 6 allora n è divisibile per 3. Quindi in questo caso quando la radice digitale di un numero e 3, 6 o 9 allora il numero è divisibile per 3.

Le radici digitali (o numeri teosofici) dei numeri primi espresse in base 10 non saranno quindi mai multipli di 3.

I numeri teosofici dei primi in base 10 non saranno quindi mai 3, 6 o 9.

Qualora i numeri fossero espressi in altre basi le loro radici numeriche non assumerebbero mai il valore della cifra più alta della base o il valore di uno dei suoi fattori o di un multiplo di uno dei fattori qualora questo sia ancora inferiore alla cifra più alta della base.  Le radici numeriche dei primi espressi in una base b possono essere unicamente i coprimi di n dove n = b − 1

In seguito è riportata una tabella delle radici mancati nei primi espressi in diverse basi numeriche. Nel caso della base 2 ogni numero ha per radice digitale il numero 1, infatti tutti i numeri sono divisibile per 1.

	Radici digitali mancanti nei primi	n=(b-1)	Possibili valori della radice digitale nei primi (coprimi di n)	Numero dei coprimi
3	2	2	1	1
4	3	3	1,2	2
5	4,2	4	1,3	2
6	5	5	1,2,3,4	4
7	6,4,3,2	6	1,5	2
8	7	7	1,2,3,4,5,6	6
9	8,6,4,2	8	1,3,5,7	4
10	9,6,3	9	1,2,4,5,7,8	6

Andamento della 𝜑(n) fino a 1000

Mandai la dimostrazione anche a Claudio che mi confermò la correttezza dei ragionamenti facendomi notare che la sequenza che avevo evidenziato era una famosa sequenza numerica molto studiata in teoria dei numeri, la sequenza numerica del numero di coprimi di un numero n chiamata funzione di Eulero 𝜑(n) o toziente.

Questa funzione fu scoperta da Eulero, matematico svizzero, che è considerato il più importante matematico del Settecento, e uno dei massimi della storia. È noto per essere tra i più prolifici di tutti i tempi e ha fornito contributi storicamente cruciali in svariate aree: analisi infinitesimale, funzioni speciali, meccanica razionale, meccanica celeste, teoria dei numeri, teoria dei grafi. Sembra che Pierre Simon Laplace abbia affermato "Leggete Eulero; egli è il maestro di tutti noi".

Eulero dimostrò che la funzione 𝜑(n), che per ogni n indica il numero dei coprimi minori di n di n, può essere espressa anche come

            

Dove p∥n sono tutti e solo i primi che contribuiscono alla fattorizzazione di n.

Eulero partì dalla constatazione che ogni numero per il teorema fondamentale dell’aritmetica può essere espresso come

dove  p_i è un primo fattore di n e r è il numero dei diversi fattori primi di n e quindi per 𝜑(n), vale 

ma la funzione 𝜑(n) di Eulero è moltiplicativa: per ogni coppia di interi 𝑎 e b che siano coprimi, cioè tali che MCD(𝑎, b)=1, si ha:

Ma i valori p_i^k_i essendo potenze di primi sono coprimi tra loro e quindi  

      

in seguito Eulero dimostra che 𝜑(p_i^k_i) può essere espresso come:

            

Infatti i numeri non coprimi di p_i^k_i essendo p_i  primo sono tutti i multipli di p_i  fino a p_i^k_i-1

p_i,  2p_i , 3p_i, ...p_i^k_i-1

Questo insieme ha p_i^k_i-1 membri

Quindi 𝜑(p_i^k_i) il numero dei coprimi di p_i^k_i, sarà dato dalla differenza tra la quantità dei numeri minore o uguale a p_i^k_i cioè  p_i^k_i e la quantità dei numeri non coprimi di p_i^k_i e quindi:

𝜑(p_i^k_i)=p_i^k_i−p_i^k_i-1

Da qui si ottiene la 8)

Ora sostituendo la 8) nella 7) si ottiene

Moltiplicando e dividendo per p_i

Per la proprietà commutativa della moltiplicazione

ma

e quindi

QED

Eulero si pose la domanda quale valore avrebbe assunto il prodottoper tutti gli infiniti numeri primi.

Ora Eulero nel 1737 dimostro che l'inversa di , ovvero  è uguale alla somma della serie armonica:

Ma la serie armonica  diverge e quindi  tende a zero.

Eulero estesa la 9) definendo la funzione ζ(x) , oggi chiamata funzione zeta o prodotto di Eulero.

Dove x e un numero reale maggiore di 1 e dimostrò che

Bernhard Riemann, matematico tedesco, in un articolo pubblicato nel 1859 dal titolo “Über die Anzahl der Primzahlen unter einer gegebenen Größe” estese la funzione zeta di Eulero nel dominio dei numeri complessi e ne studio le caratteristiche. 

La funzione zeta estesa ai numeri complessi, chiamata zeta di Riemann, come risulta dalla 9), ha un polo in Re[1]Im[0]. Inoltre gli zeri della zeta di Riemann sono di due tipi. Gli zeri cosiddetti banali che si trovano tutti sull’asse reale negativo del piano immaginario in corrispondenza dei multipli di Re[-2]Im[0]. Oltre a questi, secondo l’ipotesi formulata da Riemann, la funzione ha zeri non banali che dovrebbero trovarsi tutti sulla retta parallela all’asse imaginario passante per Re[1/2]Im[0].

La dimostrazione o la refutazione dell’ipotesi di Riemann oggi conosciuta come la congettura di Riemann è il problema più importante della teoria dei numeri e forse di tutta la matematica. La soluzione della congettura di Riemann getterebbe luce sulla legge che governa la distribuzione dei numeri primi. Si spera che dalla risoluzione e dalle conseguenze della dimostrazione possa finalmente scaturire una formula che indichi la quantità di primi minori di un numero dato. Chissà che poi questo non apri la strada per trovare il sacro Graal della matematica: la formula che esprima solo e tutti i numeri primi e che quindi squarci il velo che gli avvolge misteriosamente.

Durante le conferenze e le mostre di quel solstizio d’estate materano i numeri primi e la congettura di Riemann furono un argomento ricorrente. Tobia Ravà con la sua osservazione sulle radici numeriche dei numeri primi aveva contribuito forse più di altri alla loro poetica dando pieno senso al nome della manifestazione.